|
Определение 1. Функции F*(X1, ..., Xn) называется двойственной к функции F(X1, ..., Xn), если F*(X1, ..., Xn) =  ( (  1, ..., 1, ...,  N). N).
Пример 1. Покажем с помощью таблицы истинности, что константа 0 двойственна к 1:
Функции F(X) = X и G(X) =  двойственны сами себе: двойственны сами себе:
|
X
|
F
|
F*
|
G
|
G*
|
|
0
1
|
0
1
|
0
1
|
1
0
|
1
0
|
Так как F*(0)=  (1). (1).
Определение 2. Если F*(X1, ..., Xn) = F(X1, ..., Xn), то F(X1, ..., Xn) называется самодвойственной.
Пример 2. Покажем, что F(X1,X2,X3)=X1ÅX2ÅX3 – самодвойственна:
|
X1
|
X2
|
X3
|
F
|
F*
|
|
0
0
0
0
1
1
1
1
|
0
0
1
1
0
0
1
1
|
0
1
0
1
0
1
0
1
|
0
1
1
0
1
0
0
1
|
0
1
1
0
1
0
0
1
|
Если F*– самодвойственна, то  ( (  1, ..., 1, ...,  n) = F(X1, ..., Xn), т. е. на противоположных наборах функция принимает противоположные значения. n) = F(X1, ..., Xn), т. е. на противоположных наборах функция принимает противоположные значения.
Пример 3. Покажем, что функция Х1ÚХ2 двойственна к X1&X2, функция Х1 Х2 двойственна к функцииX1|X2.
|
X1 X2
|
F=Х1ÚХ2
|
F*
|
G=X1|X2
|
G*=X1 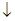 X2 X2
|
|
0 0
0 1
1 0
1 1
|
0
1
1
1
|
0
0
0
1
|
1
1
1
0
|
1
0
0
0
|
Теорема о двойственных функциях
Если F* двойственна к F, то F двойственна к F*.
Доказательство. F*(X1, ..., Xn) =  ( (  1, ..., 1, ...,  N). Найдем двойственную функцию к F*, т. е. (F*( X1, ...,Xn))* = ( N). Найдем двойственную функцию к F*, т. е. (F*( X1, ...,Xn))* = (  ( (  1, ..., 1, ...,  N))* = N))* =  ( (  1, ..., 1, ...,  N) = F(X1, .., Xn). N) = F(X1, .., Xn).
Предположим, что функция задана формулой. Можно ли найти по этой формуле двойственную функцию? Ответ на этот вопрос дает следующая теорема.
Принцип двойственности
Теорема: Пусть функция H(X1, ..., Xn) реализована формулой H(X1, ..., Xn) = =G(G1, ..., Gm) = G(F1(X1, ...,Xn), ..., Fm(X1, ..., Xn)), где какие-то переменные могут быть фиктивными. Тогда H*( x1, ..., Xn) = G*(F1*( X1, ..., Xn), ..., Fm*(X1, …, Xn)), это означает, что если функция задана некоторой формулой, то чтобы получить двойственную функцию, надо в этой формуле все знаки функций заменить на двойственные, 0 на 1, 1 на 0.
Доказательство. H*(X1, ..., Xn) =  ( (  1, ..., 1, ...,  n) = n) =  (F1( (F1(  1, ..., 1, ...,  n), ..., Fm( n), ..., Fm(  1, ..., 1, ...,  n)) = n)) =  ( (  1( 1(  1, ..., 1, ...,  n), ..., n), ...,  ( (  1, ..., 1, ...,  n)) = G(( n)) = G((  ), ..., (( ), ..., ((  ) = G*(F1*( X1, ..., Xn), ..., Fm*( X1, ..., Xn)), что и требовалось доказать. ) = G*(F1*( X1, ..., Xn), ..., Fm*( X1, ..., Xn)), что и требовалось доказать.
Если функция H(X1, ..., Xn) реализуется формулой N[F1, ..., Fn], то формулу, полученную из N заменой Fi, входящих в нее, на Fi* и реализующую функцию H*(X1, ..., Xn), будем называть двойственной и обозначатьN*(X1, ..., Xn).
Пример 4. Построить формулу, реализующую F*, если F = ((X 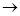 Y) Ú Z) (Y Y) Ú Z) (Y  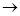 (XÅYz)). Покажем, что она эквивалентна формуле N = Z(XÅY). (XÅYz)). Покажем, что она эквивалентна формуле N = Z(XÅY).
Найдем (XÅY)* и (X 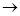 Y)*. Y)*.
|
X y
|
XÅY
|
(XÅY)*
|
X 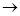 Y Y
|
(X 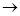 Y)* Y)*
|
|
0 0
0 1
1 0
1 1
|
0
1
1
0
|
1
0
0
1
|
1
1
0
1
|
0
1
0
0
|
Из таблиц видно, что
(X  Y)* = X ~ Y = Y)* = X ~ Y =  = X = X  Y Y  1, X 1, X  Y = Y =  Y Y  X X  , ,
(X 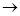 Y)* = Y)* =  Y X Y X 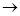 Y = Y =   Y. Y.
По принципу двойственности:
F* =  Yz Yz  ( (  (X (X  (Y (Y  Z) Z)  1)) = 1)) =  Yz Yz   Z(X Z(X  (Y (Y  Z) Z)  1) = Z( 1) = Z(  YÚ( YÚ(  XÅ XÅ  ZÅ ZÅ  )) =Z( )) =Z(  YÚ YÚ  (XÅZÅ1)) = Z( (XÅZÅ1)) = Z(  YÚ YÚ  (XÅ (XÅ  )) = Z )) = Z  YÚ(Z YÚ(Z  XÅZ XÅZ   ) = Z( ) = Z(  YÚX YÚX  ) = Z(XÅY). ) = Z(XÅY).
Тогда F = (F*)* = [Z(XÅY)]* = ZÚ(X~Y).
Пример 5. Найти формулу для f* и показать, что она эквивалентна формуле N = (XÚ(ZÅT))  , если F = (Xyz~(TÚX , если F = (Xyz~(TÚX  ))Ú ))Ú  T. T.
F* = ((XÚYÚZ)ÅT(  ÚY))( ÚY))(  ÚT) = ( ÚT) = (  T( T(  ÚY)Ú(XÚYÚZ) ÚY)Ú(XÚYÚZ)  )( )(  ÚT) = ÚT) =
= (    TÚ(XÚYÚZ)( TÚ(XÚYÚZ)(  ÚX ÚX  ))( ))(  ÚT) = ÚT) =    TÚ(XÚYÚZ)( TÚ(XÚYÚZ)(   ÚX ÚX  ÚTx ÚTx  ) = ) =
=    TÚ(XÚYÚZ)( TÚ(XÚYÚZ)(   ÚX ÚX  ) = ) =  ( (  XÚ XÚ  TÚ TÚ  ZÚXÚXz) = ZÚXÚXz) =  ( (  TÚXÚ TÚXÚ  ZÚXz) ZÚXz)
=  (XÚ(ZÅT)). (XÚ(ZÅT)).
Лемма о несамодвойственной функции
Подстановкой функций  и и  в несамодвойственную функцию можно получить одну из констант. в несамодвойственную функцию можно получить одну из констант.
Доказательство. Пусть  – несамодвойственная функция. Тогда существует набор – несамодвойственная функция. Тогда существует набор  , для которого , для которого  . Построим функцию . Построим функцию  , заменив единицы в , заменив единицы в  на на  , а нули – на , а нули – на  . Так как . Так как  , то , то  . Заметим, что . Заметим, что  . .
Тогда  , т. е. , т. е.  . Следовательно, функция . Следовательно, функция  есть одна из констант. есть одна из констант.
Эквивалентность формул и нормальные формы
|
