Бинарное (или двоичное) дерево — это непустое конечное множество узлов, на котором определена структура, обладающая следующими свойствами:

1. Имеется один выделенный узел г, называемый корнем данного бинарного дерева.

2. Остальные узлы (исключая корень) содержатся в двух непересекающихся множествах (поддеревьях) — левом и правом, каждое из которых, в свою очередь, либо пусто, либо является бинарным деревом.

На первый взгляд может показаться, что бинарное дерево — это частный случай упорядоченного ориентированного дерева, в котором у каждого узла не более двух смежных. Но это не так, бинарное дерево не является упорядоченным ордеревом. Дело в том, что даже если у некоторого узла бинарного дерева имеется только одно непустое поддерево, то всё равно известно, какое именно это поддерево: левое или правое.

Пример

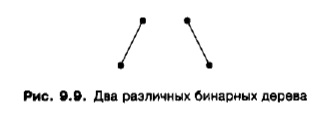
На рис. 9.9 приведены две диаграммы деревьев, которые изоморфны как упорядоченные, ориентированные и свободные деревья, но не изоморфны как бинарные деревья.

ЗАМЕЧАНИЕ

Понятие двоичного дерева допускает обобщение, m-ичным деревом называется непустое конечное множество узлов, которое состоит из корня и m непересекающихся подмножеств, имеющих номера 1,...,m, каждое из которых в свою очередь, либо пусто, либо является m-ичиым деревом. Большая часть утверждений и алгоритмов для двоичных деревьев может быть сравнительно легко распространена и на m-ичные деревья(с соответствующими модификациями). Поэтому хотя на практике m-ичные деревья и используются достаточно часто, здесь мы ограничиваемся только двоичными деревьями.

Дерево — это связный ациклический граф. Связность означает наличие путей между любой парой вершин, ацикличность — отсутствие циклов и то, что между парами вершин имеется только по одному пути.

Ориентированное (направленное) дерево — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями.

Формально дерево определяется как конечное множество   одного или более узлов со следующими свойствами:

существует один корень дерева 

остальные узлы (за исключением корня) распределены среди   непересекающихся множеств  , и каждое из множеств является деревом; деревья   называются поддеревьями данного корня  .

Основные определения

Степень узла — количество исходящих дуг (или, иначе, количество поддеревьев узла).

Концевой узел (лист, терминальная вершина) — узел со степенью 1 (то есть узел, в который ведёт только одно ребро; в случае ориентированного дерева — узел, в который ведёт только одна дуга и не исходит ни одной дуги).

Узел ветвления — не концевой узел.

Уровень узла — длина пути от корня до узла. Можно определить рекурсивно:

уровень корня дерева   равен 0;

уровень любого другого узла на единицу больше, чем уровень корня ближайшего поддерева дерева  , содержащего данный узел.

Дерево с отмеченной вершиной называется корневым деревом.

-й ярус дерева   — множество узлов дерева, на уровне   от корня дерева.

частичный порядок на вершинах:  , если вершины   и   различны и вершина   лежит на (единственной!) элементарной цепи, соединяющей корень с вершиной  .

корневое поддерево с корнем   — подграф  .

Остовное дерево (остов) — это подграф данного графа, содержащий все его вершины и являющийся деревом. Рёбра графа, не входящие в остов, называются хордами графа относительно остова.

Лес — множество (обычно упорядоченное), не содержащее ни одного непересекающегося дерева или содержащее несколько непересекающихся деревьев.