Граф без циклов называется ациклическим, или лесом. Связный ациклический граф называется (свободным) деревом. Таким образом, компонентами связности леса являются деревья.

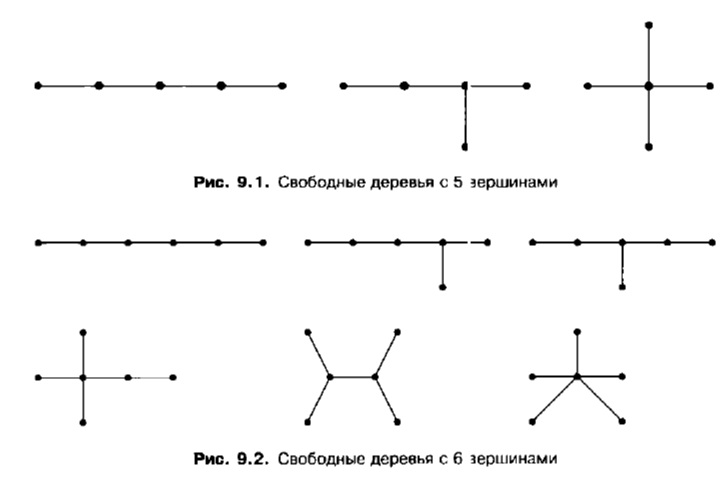
Основные свойства деревьев

Следующая теорема устанавливает, что два из четырех свойств — связность, ацикличность, древочисленность и субцикличикличность — характеризуют граф как дерево.

ТЕОРЕМА

Пусть G(V, Е) — граф ср вершинами, q ребрами, к компонентами связности и z простыми циклами. Пусть далее х — ребро, соединяющее любую пару несмежных вершин в G. Тогда следующие утверждения эквивалентны:

1. G — дерево, то есть связный граф без циклов,

2. Любые две вершины соединены в G единственной простой цепью

3. G — связный граф, и любое ребро есть мост

4. G — связный и древочисленный

5. G — ациклический и древочисленный

6. G — ациклический и субциклический

7. G — связный, субциклический и неполный

8. G — древочисленный и субциклический (за двумя исключениями)

С Л Е Д С Т В И Е 1

В любом нетривиальном дереве имеются по крайней мере две висячие вершины.

З А М Е Ч А Н И Е

Легко видеть, в частности, что висячими вершинами в дереве являются концы любого диаметра.

С Л Е Д С Т В И Е 2

Каждая не висячая вершина свободного дерева является точкой сочленения.

С Л Е Д С Т В И Е 3

Если в связном графе нет висячих вершин, то в нём есть цикл. ДОКАЗАТЕЛЬСТВО ОТ противного. Если связный граф не имеет циклов, то он является деревом, и по следствию 1 обязан иметь висячие вершины. 

Центр дерева

Свободные деревья выделяются из других графов тем, что их центр всегда оправ-дывает своё название.

Т Е О Р Е М А

Центр свободного дерева состоит из одной вершины или из двух смежных вершин